Rectangle vs. Parallelogram: You Won't Believe the Difference!

Geometry, a branch of mathematics, studies shapes like rectangles and parallelograms. Rectangles, often explored in elementary mathematics, are quadrilaterals with specific properties. Parallelograms, in contrast, represent a broader category of quadrilaterals. Understanding what is the difference between a rectangle and a parallelogram requires examining their respective angles and side lengths. Euclid's Elements provides foundational principles for understanding these geometric figures.

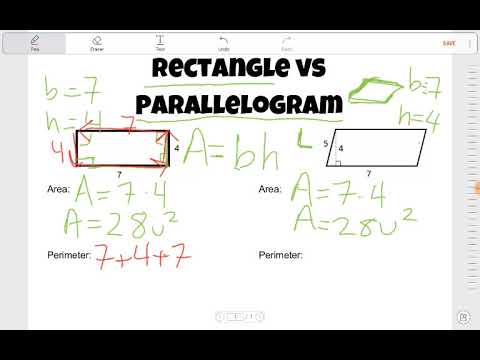
Image taken from the YouTube channel The Free Math Tutor , from the video titled What is a RECTANGLE, anyway? Part 3: Is a Rectangle a Parallelogram? Is a Parallelogram a Rectangle? .
Rectangle vs. Parallelogram: Unveiling the Key Difference
This article explores the specific characteristic that distinguishes a rectangle from a parallelogram. While both shapes share several properties, understanding their unique attributes is crucial for accurate identification.
Understanding Parallelograms
A parallelogram is a four-sided shape (quadrilateral) with two pairs of parallel sides. "Parallel" means the sides will never intersect, no matter how far they are extended.
-
Key Properties of a Parallelogram:
- Opposite sides are parallel.
- Opposite sides are equal in length.
- Opposite angles are equal.
- Adjacent angles are supplementary (add up to 180 degrees).
- Diagonals bisect each other (cut each other in half).
Defining Rectangles
A rectangle is also a quadrilateral with two pairs of parallel sides. It inherits all the properties of a parallelogram but possesses an additional, defining characteristic.
-
Key Properties of a Rectangle:
- All properties of a parallelogram.
- All four angles are right angles (90 degrees).
What is the Difference Between a Rectangle and a Parallelogram?
The core difference lies in the angles.
- Angle Requirement: A rectangle must have four right angles. A parallelogram, on the other hand, can have angles of any measure, as long as opposite angles are equal and adjacent angles are supplementary.
Illustrative Table
| Feature | Parallelogram | Rectangle |
|---|---|---|
| Parallel Sides | Two pairs of parallel sides | Two pairs of parallel sides |
| Equal Sides | Opposite sides are equal | Opposite sides are equal |
| Equal Angles | Opposite angles are equal | Opposite angles are equal |
| Right Angles | Not necessarily | Four right angles (90 degrees) |
| Diagonals | Bisect each other | Bisect each other and are congruent |
The Hierarchy: A Rectangle is a Special Parallelogram
Essentially, a rectangle is a special type of parallelogram. It’s a parallelogram that happens to have four right angles. Therefore, all rectangles are parallelograms, but not all parallelograms are rectangles. Consider it like this:
- Parallelogram: The broad category of four-sided shapes with two pairs of parallel sides.
- Rectangle: A specific type of parallelogram that adheres to the additional rule of having four right angles.
Think of squares similarly. A square is a special type of rectangle with four equal sides.
Video: Rectangle vs. Parallelogram: You Won't Believe the Difference!
Rectangle vs. Parallelogram: FAQs
Here are some frequently asked questions to help clarify the distinctions between rectangles and parallelograms.
Is every rectangle also a parallelogram?
Yes, a rectangle is a parallelogram. A rectangle meets all the criteria to be a parallelogram: opposite sides are parallel and equal in length. It simply has the added requirement of having four right angles.
What distinguishes a rectangle from other parallelograms?
The key difference between a rectangle and a parallelogram lies in their angles. A rectangle must have four right angles (90 degrees). A parallelogram can have angles of any measure, as long as opposite angles are equal. Therefore, what is the difference between a rectangle and a parallelogram is that a rectangle is an equiangular parallelogram.
Can a parallelogram be a rectangle if its sides are not the same length?
Absolutely! The lengths of the sides don't dictate whether a parallelogram is a rectangle. The determining factor is whether all four angles are right angles. It's perfectly acceptable for a rectangle's length and width to be different.
Does a square also fit into both categories?
Yes, a square is both a rectangle and a parallelogram. It satisfies the requirements of both: opposite sides are parallel and equal (parallelogram), and all four angles are right angles (rectangle). It also has the added feature that all four sides are equal in length.