Unlock BCC Volume: Simple Guide & Formula (Must-Know!)

Crystallography, a branch of materials science, provides the framework for understanding the atomic arrangement within materials. The body-centered cubic (BCC) structure, a common arrangement found in metals like iron, exhibits unique properties that are directly influenced by its atomic packing. Determining the volume of body centered cubic unit cell is therefore crucial for predicting material behavior. This fundamental calculation, utilizing knowledge of the atomic radius, allows engineers and scientists to analyze density and other critical characteristics. This article provides a simple guide and the essential formula to Unlock BCC Volume.
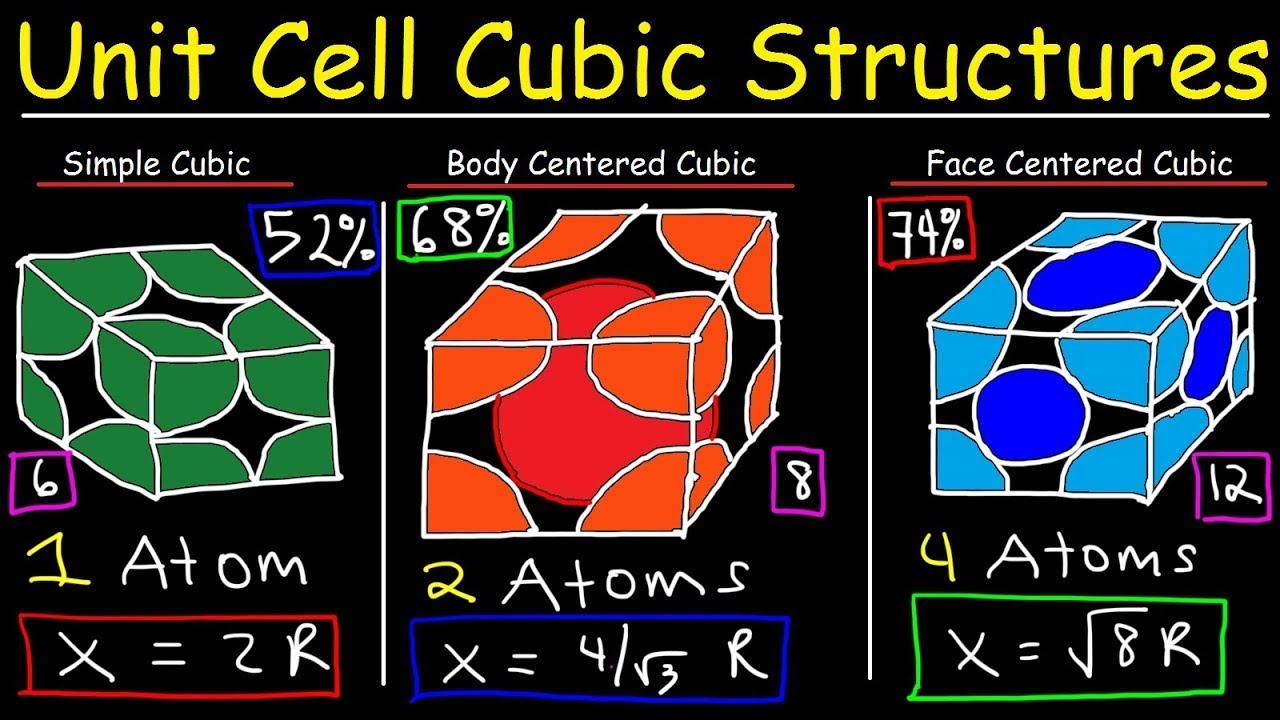
Image taken from the YouTube channel The Organic Chemistry Tutor , from the video titled Unit Cell Chemistry Simple Cubic, Body Centered Cubic, Face Centered Cubic Crystal Lattice Structu .
Understanding and Calculating the Volume of a Body-Centered Cubic (BCC) Unit Cell
This guide provides a clear explanation and formula for determining the volume of a body-centered cubic (BCC) unit cell. We will explore the structure of a BCC unit cell and derive the essential relationship between its edge length and atomic radius, ultimately leading to the volume calculation.
What is a Body-Centered Cubic (BCC) Unit Cell?
A body-centered cubic (BCC) unit cell is a type of crystal structure commonly found in metals. It is characterized by atoms located at each of the eight corners of a cube, with an additional atom positioned at the very center of the cube.
Key Characteristics of BCC Structure:
- Atoms at Corners: Each corner atom is shared by eight adjacent unit cells.
- Atom at Center: The atom located at the center belongs entirely to that specific unit cell.
- Packing Efficiency: BCC structures have a relatively lower packing efficiency compared to face-centered cubic (FCC) structures. This means there is more "empty space" in a BCC structure.
Determining the Number of Atoms per BCC Unit Cell
To understand the atomic packing, it's crucial to know how many atoms effectively belong to each unit cell.
-
Corner Atoms: Since each corner atom is shared by eight unit cells, each contributes 1/8 of an atom to the unit cell. With eight corners, this contributes 8 * (1/8) = 1 atom.
-
Center Atom: The atom in the center belongs entirely to the unit cell, contributing 1 atom.
-
Total Atoms: Therefore, each BCC unit cell effectively contains 1 (from corners) + 1 (from center) = 2 atoms.
Relationship Between Edge Length (a) and Atomic Radius (r) in a BCC Unit Cell
The key to calculating the volume of a BCC unit cell lies in understanding the relationship between its edge length a and the atomic radius r of the atoms it contains. This relationship is derived by considering the atoms that touch along the body diagonal of the cube.
Deriving the a-r Relationship:
- Body Diagonal: The body diagonal of the cube passes through the center atom and two corner atoms. These atoms touch each other along this diagonal.
- Diagonal Length: The length of the body diagonal is 4r, as it consists of the radii of two corner atoms (r each) and the diameter of the central atom (2r).
- Using Pythagorean Theorem: The body diagonal can also be expressed in terms of the edge length a using the Pythagorean theorem applied twice. First, consider the face diagonal, which has a length of √2 a. Then, using the face diagonal and the edge length a as two sides of a right triangle, the body diagonal has a length of √((√2 a)² + a²) = √(3 a²)= a*√3.
- Equating: Therefore, we have a√3 = 4r.
- Solving for a: This gives us the relationship a = (4r) / √3.
- Solving for r: Equivalently, r = (a√3) / 4.
Formula for the Volume of a BCC Unit Cell
Now that we have the relationship between the edge length (a) and the atomic radius (r), we can calculate the volume of the BCC unit cell.
Volume Calculation:
-
Volume Formula: The volume (V) of a cube is simply the edge length cubed: V = a³.
-
Expressing Volume in terms of a: If the edge length a is known, the volume calculation is straightforward.
-
Expressing Volume in terms of r: If only the atomic radius r is known, we substitute the expression for a in terms of r into the volume formula:
V = a³ = ((4r) / √3)³ = (64r³) / (3√3)
Summary of Formulas:
| Variable(s) Known | Volume Formula |
|---|---|
| Edge Length (a) | V = a³ |
| Atomic Radius (r) | V = (64r³) / (3√3) ≈ 12.32r³ |
Example Calculations
Let's illustrate the calculation of the volume with some examples.
Example 1: Given Edge Length
If the edge length a of a BCC unit cell is 4 Å (Angstroms), the volume is:
V = a³ = (4 Å)³ = 64 ų
Example 2: Given Atomic Radius
If the atomic radius r of a BCC metal is 1.5 Å, the volume is:
V = (64r³) / (3√3) = (64 (1.5 Å)³) / (3√3) ≈ (64 3.375 ų) / 5.196 ≈ 41.57 ų

Video: Unlock BCC Volume: Simple Guide & Formula (Must-Know!)
FAQs: Understanding BCC Volume
Hopefully, this FAQ section will clarify any confusion about calculating the volume of a body centered cubic unit cell. Let's dive in!
What exactly is a Body Centered Cubic (BCC) structure?
A Body Centered Cubic (BCC) structure is a type of crystal structure found in some metals. It has one atom at each of the eight corners of the cube, and one atom at the center of the cube. This arrangement affects its properties, including its volume.
Why is knowing the volume of a BCC unit cell important?
Calculating the volume of a body centered cubic unit cell helps determine density, atomic packing factor, and other material properties. This is crucial in materials science and engineering for predicting material behavior and performance.
How does the atomic radius relate to the volume of the BCC unit cell?
The atomic radius (r) is crucial in determining the edge length (a) of the BCC unit cell. In a BCC structure, 4r = a√3. Once 'a' is known, the volume of the body centered cubic unit cell is simply a³.
I'm still struggling with the formula. Can you re-explain it simply?
Okay, here's the simplified breakdown: First, find the atomic radius (r). Then, calculate the edge length (a) using a = 4r/√3. Finally, cube the edge length (a) to get the volume of the body centered cubic unit cell: Volume = a³.
