Unlock the Mystery: What is the Range of a Function?

Functions, cornerstones of mathematics, describe relationships between sets. Understanding their behavior often requires determining the range of the function, which represents all possible output values. This determination involves carefully analyzing the domain, the set of allowable inputs. Graphing calculators, such as those offered by TI (Texas Instruments), serve as valuable tools for visualizing these relationships. Moreover, George Boole's work on Boolean Algebra laid crucial groundwork that continues to influence modern mathematical analysis related to what is the range of the function ?

Image taken from the YouTube channel Khan Academy , from the video titled What is the range of a function? | Functions | Algebra I | Khan Academy .
Unlock the Mystery: What is the Range of a Function?
Understanding the range of a function is crucial for grasping how functions behave and what outputs they produce. Let's explore this concept in detail.
Defining the Range of a Function
At its core, the range of a function is the set of all possible output values (also known as dependent variables) that the function can produce. Imagine a function as a machine: you feed it an input, and it spits out an output. The collection of all the possible things this machine can spit out is the range.
Distinguishing Range from Other Function Concepts
It's important to distinguish the range from related concepts like the domain and codomain.
- Domain: This is the set of all possible input values that the function can accept.
- Codomain: This is the set of all possible potential output values. The range is always a subset of the codomain. Think of the codomain as the container the range lives inside. Not every element of the codomain has to be a value in the range, but every value in the range must be in the codomain.
To illustrate the difference, consider a function that squares any real number (f(x) = x2)
| Concept | Description | Example (f(x) = x2) |
|---|---|---|
| Domain | All possible input values. | All real numbers. |
| Codomain | The set of all potential output values (usually explicitly defined). | All real numbers. |
| Range | The actual set of all output values the function produces. | All non-negative real numbers. |
Methods for Finding the Range
Determining the range of a function varies in complexity depending on the function itself. Here are several approaches you can take:
1. Analyzing Simple Functions
For straightforward functions, you can often deduce the range by inspection or basic reasoning.
- Example: f(x) = x + 5. Since x can be any real number, adding 5 to it will also result in any real number. Therefore, the range is all real numbers.
- Example: f(x) = c, where c is a constant. The output is always c, regardless of the input. The range is simply {c}.
2. Graphical Analysis
Visualizing the function's graph is a powerful way to determine its range.
- Plot the function on a coordinate plane.
- Identify the lowest and highest y-values the graph reaches.
- The interval between these y-values represents the range.
3. Algebraic Manipulation
In some cases, rearranging the function equation can help reveal the range.
- Example: Consider the function f(x) = 1/(x-2).
- To find the range, solve for x in terms of y: y = 1/(x-2) => x-2 = 1/y => x = (1/y) + 2
- From this, we see that y can be any real number except 0 (because you can't divide by 0). Therefore, the range is all real numbers except 0.
4. Considering Function Properties
Certain function types have predictable range limitations:
- Absolute Value Functions: f(x) = |x| always produces non-negative values. Therefore, the range is typically [0, ∞) (or a subset of this depending on transformations).
- Square Root Functions: f(x) = √x (for real numbers) produces non-negative values. Therefore, the range is typically [0, ∞) (or a subset of this depending on transformations).
- Trigonometric Functions: sin(x) and cos(x) always have a range of [-1, 1]. tan(x) has a range of all real numbers.
5. Dealing with Restrictions and Discontinuities
Pay close attention to any restrictions on the domain, as these directly affect the range. Also, consider any points of discontinuity (like vertical asymptotes in rational functions), as these can exclude certain values from the range.

- Vertical Asymptotes: Often indicate values not in the range of rational functions.
- Holes: Represent a single, specific value missing from the range.
Examples to Solidify Understanding
Let's examine a few more examples:
-
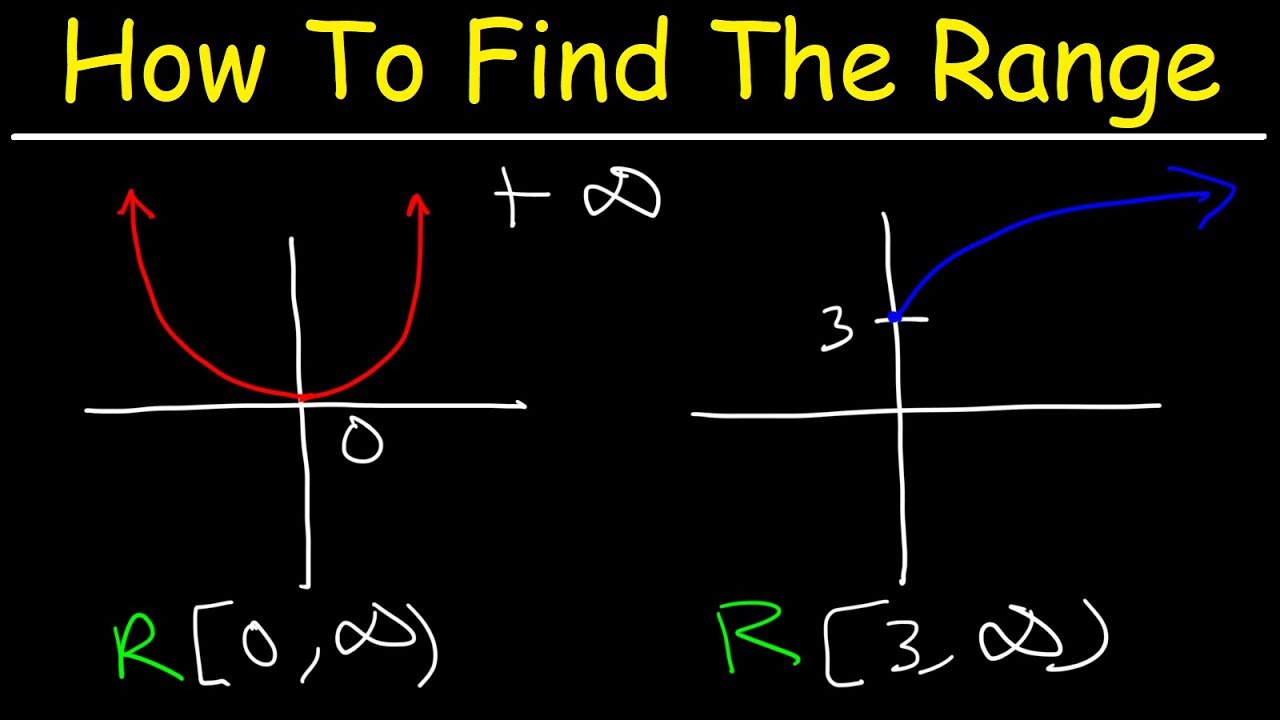
f(x) = x2 + 3: The smallest value x2 can be is 0 (when x = 0). Therefore, the smallest value of f(x) is 0 + 3 = 3. The range is [3, ∞).
-
f(x) = √(4 - x2): This is a semicircle with radius 2, centered at the origin, and lying above the x-axis. The possible output values range from 0 to 2. The range is [0, 2].
-
f(x) = (x + 1) / (x - 2): As x approaches 2, f(x) approaches infinity (positive or negative). This function has a horizontal asymptote at y = 1, meaning f(x) will never exactly equal 1. Therefore, the range is all real numbers except 1.
Video: Unlock the Mystery: What is the Range of a Function?
FAQs About Finding the Range of a Function
Here are some frequently asked questions to further clarify understanding of a function's range, which represents all possible output values.
How does the range differ from the domain of a function?
The domain is the set of all possible input values for a function, while the range represents all possible output values. Think of it this way: the domain goes into the function, and the result coming out is what is the range of the function.
What are some methods for determining the range of a function?
Several methods exist. You can analyze the function's graph, look for maximum and minimum values, consider any restrictions on the output, or solve for the independent variable to see which values are possible outputs. Understanding the function type (e.g., quadratic, exponential) also provides clues to what is the range of the function.
Can a function have an empty range?
Yes, although it's uncommon in practical applications. A function with an empty range has no possible output values. This could happen, for example, if you define a function with contradictory conditions that make it impossible to produce any value, therefore what is the range of the function is empty.
What happens if a function is defined piecewise? How do I find its range then?
For piecewise functions, you need to determine the range of each piece separately and then combine those ranges to find the overall range of the function. Be mindful of any overlaps or gaps between the individual ranges to determine what is the range of the function accurately.
So, that’s the lowdown on what is the range of the function ?. Hopefully, you’re feeling a bit more confident navigating those tricky function outputs now! Happy calculating!