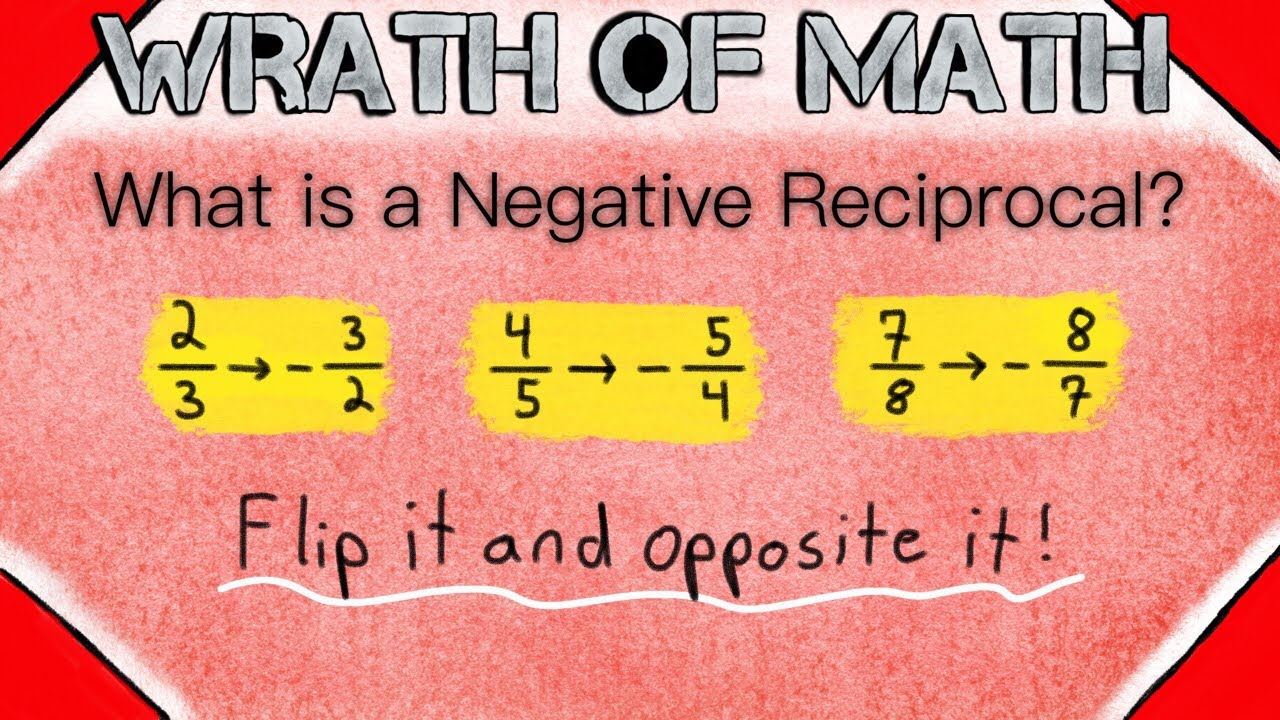Negative Number Reciprocals? Unlock the Secrets Now!

Understanding negative number reciprocals is a foundational element within the broader field of mathematical inverses. Rational numbers form the basis for comprehending both negative numbers and their reciprocals, showcasing how fraction manipulation is crucial. The principles involved have practical applications across various scientific disciplines, particularly in physics. So, as you delve into this article, grasp what is the reciprocal of a negative number and see how it connects with these fundamental concepts.
Image taken from the YouTube channel David May , from the video titled What is a Negative Reciprocal? | Dave May Teaches .
Unveiling the Mysteries of Negative Number Reciprocals
This article aims to provide a comprehensive understanding of reciprocals, specifically focusing on what happens when dealing with negative numbers. We'll explore the fundamental concept of reciprocals and then delve into how negativity affects the result.
Understanding Reciprocals: A Foundation
At its core, a reciprocal (also known as a multiplicative inverse) is a number which, when multiplied by the original number, yields the product of 1.
- Definition: For any number 'x' (excluding zero), its reciprocal is '1/x'.
- Purpose: Reciprocals are crucial in various mathematical operations, particularly division. Dividing by a number is equivalent to multiplying by its reciprocal.
Illustrative Examples of Positive Number Reciprocals
Let's consider some positive numbers and their corresponding reciprocals:
| Number (x) | Reciprocal (1/x) | Product (x * 1/x) |
|---|---|---|
| 2 | 1/2 | 1 |
| 5 | 1/5 | 1 |
| 0.25 (1/4) | 4 | 1 |
| 10 | 1/10 | 1 |
What is the Reciprocal of a Negative Number?
Now, let's address the main topic: "what is the reciprocal of a negative number?". The reciprocal of a negative number is also a negative number. This follows directly from the definition of a reciprocal. To obtain a product of 1 when multiplying, a negative number must be multiplied by another negative number (since a positive times a negative yields a negative product).
Finding the Reciprocal of a Negative Number: The Process
- Identify the Number: Determine the negative number for which you want to find the reciprocal.
- Express as a Fraction (if necessary): If the number is a decimal, convert it into a fraction for easier manipulation.
- Apply the Reciprocal Rule: Replace 'x' with '-x' in the reciprocal formula (1/x), resulting in 1/(-x), which simplifies to - (1/x). Therefore, the reciprocal of -x is - (1/x).
- Simplify (if possible): Reduce the resulting fraction to its simplest form.
Examples of Negative Number Reciprocals
Here are several examples to solidify your understanding:
- Example 1: Find the reciprocal of -3.
- Following the rule, the reciprocal is - (1/3).
- Example 2: Find the reciprocal of -0.5 (which is -1/2).
- The reciprocal is - (1/(-1/2)) = - (-2) = -2.
- Example 3: Find the reciprocal of -4/5.
- The reciprocal is - (1/(-4/5)) = - (-5/4) = -5/4.
Why the Reciprocal of a Negative Number is Always Negative
Mathematically, this stems from the rules of multiplication involving negative numbers.
- A positive number multiplied by a positive number results in a positive number.
- A negative number multiplied by a negative number results in a positive number.
- A positive number multiplied by a negative number results in a negative number.
Since we need a product of +1 (positive one) to satisfy the definition of a reciprocal, a negative number must be multiplied by another negative number. Therefore, the reciprocal of any negative number is always negative.
Video: Negative Number Reciprocals? Unlock the Secrets Now!
Negative Number Reciprocals: Your Questions Answered
Got questions about negative number reciprocals? This FAQ section clarifies common points and helps solidify your understanding.
How do you find the reciprocal of a negative number?
To find the reciprocal of a negative number, simply find the reciprocal of its positive counterpart and keep the negative sign. For example, the reciprocal of -2 is -1/2.
Is the reciprocal of a negative number always negative?
Yes, the reciprocal of a negative number is always negative. Taking the reciprocal simply inverts the number, but doesn't change its sign. If you start with a negative number, you end up with a negative number.
What is the reciprocal of a negative number like -1/4?
The reciprocal of -1/4 is -4. Remember to flip the fraction and keep the negative sign. What is the reciprocal of a negative number is a simple inverting process with the same sign.
What happens if I take the reciprocal of zero?
Zero does not have a reciprocal. Attempting to find the reciprocal of zero involves dividing by zero, which is undefined in mathematics. Therefore, there is no such thing as the reciprocal of zero.
Alright, now you've got a good handle on what is the reciprocal of a negative number! Go forth and conquer those math problems, and remember, even negative numbers have a positive side... eventually. Happy calculating!