Negative Reciprocal? Easy Guide You'll Wish You Knew!

Understanding slopes represents a core concept in linear equations, often visualized on a Cartesian plane. The concept of perpendicular lines, frequently explored in Euclidean geometry, directly relates to negative reciprocals. This easy guide simplifies the process; and by grasping these relationships, you'll master how to find a negative reciprocal, a skill useful for solving a multitude of geometric problems.

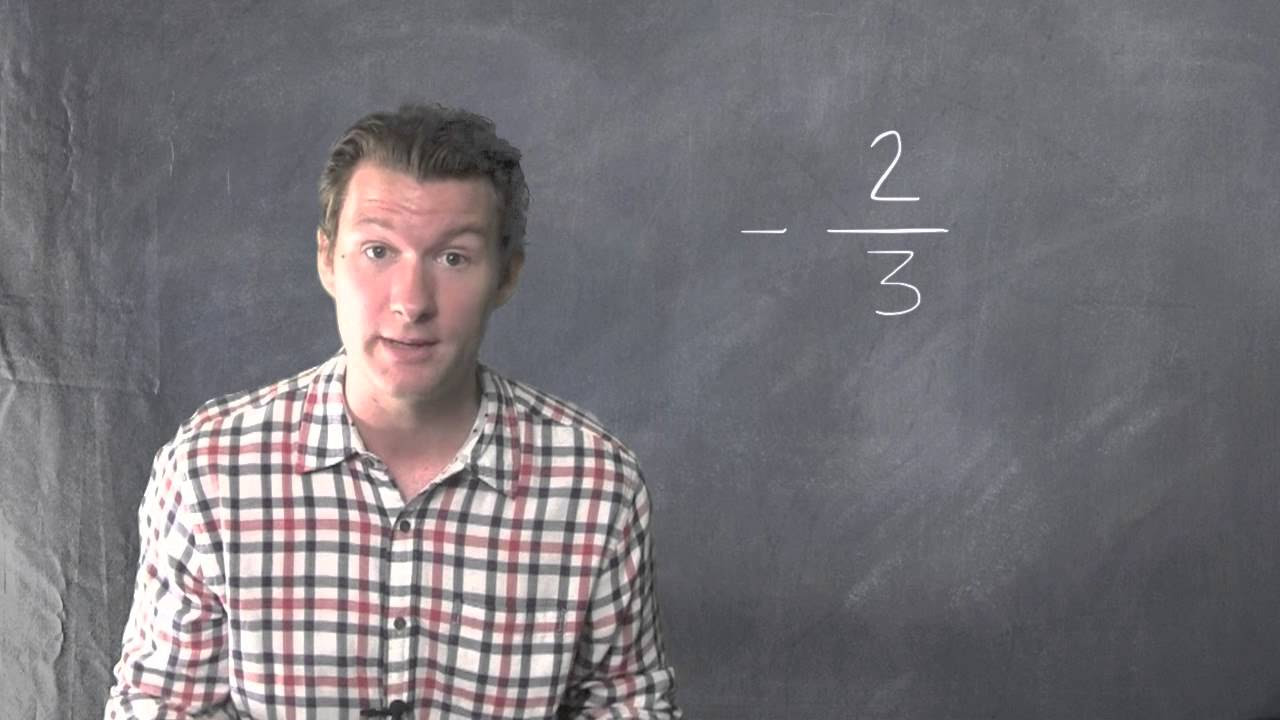
Image taken from the YouTube channel David May , from the video titled What is a Negative Reciprocal? | Dave May Teaches .

Negative reciprocals might sound intimidating, but they are a fundamental concept with wide-ranging applications. This seemingly complex term represents a simple yet powerful mathematical relationship. Understanding negative reciprocals unlocks doors to solving problems in geometry, algebra, and even real-world scenarios.

At its core, the concept of a negative reciprocal builds upon the familiar idea of a reciprocal. We'll explore this relationship thoroughly, but it's essential to understand from the outset that it involves two key actions: inversion and negation.

Defining the Negative Reciprocal

A negative reciprocal is created by first finding the reciprocal of a number. Then, you reverse its sign. So, a positive number becomes negative, and a negative number becomes positive. This simple transformation unlocks a wealth of mathematical possibilities.

Why is understanding negative reciprocals so important? Because they provide a key to understanding perpendicularity. Perpendicular lines form right angles, and the slopes of perpendicular lines are always negative reciprocals of each other.

The Importance in Mathematics and Related Fields

The concept of negative reciprocals extends far beyond basic arithmetic.

In Geometry, they are crucial for determining if two lines are perpendicular. This is essential in everything from architectural design to computer graphics.

In Algebra, negative reciprocals appear in various contexts, including solving equations and analyzing functions.

Furthermore, in Calculus, understanding negative reciprocals is essential for working with derivatives and integrals. They play a role in finding normal lines to curves and analyzing rates of change.

Real-World Applications

The utility of negative reciprocals isn't confined to the classroom. They appear in various real-world applications:

• Construction: Builders use negative reciprocals to ensure walls are perpendicular and structures are stable. Accurate angles are vital for safety and structural integrity.

• Navigation: Sailors and pilots rely on negative reciprocals when calculating headings and courses, especially when dealing with right angles and perpendicular paths.

• Engineering: Engineers use negative reciprocals in various calculations, particularly when designing structures and systems that involve perpendicular components.

The applications of negative reciprocals are diverse and impactful, highlighting their importance in numerous fields that shape our world. Mastering this concept provides a distinct advantage in problem-solving and critical thinking across many disciplines.

The utility of negative reciprocals isn't confined to the classroom. It plays an essential role in many real-world applications. However, before we delve deeper into negative reciprocals, we must first understand the concept of a reciprocal. This is the foundation upon which our understanding of negative reciprocals will be built.

What is a Reciprocal? A Foundation for Understanding

At its heart, a reciprocal is one of the simplest yet most useful concepts in mathematics. It's a tool we use constantly, even if we don't always realize it. Let's break down what it means and how to find it.

Defining the Reciprocal

In simple terms, the reciprocal of a number is what you multiply that number by to get 1. It's also commonly referred to as the multiplicative inverse. Think of it as "flipping" the number. The reciprocal of a number, x, is simply 1/x.

Finding the Reciprocal of a Number

To find the reciprocal of a number, you simply divide 1 by that number. This might sound complex, but it's a straightforward process.

Reciprocals of Fractions

For fractions, finding the reciprocal is incredibly easy. You simply invert the fraction – switch the numerator and the denominator.

For example, the reciprocal of 2/3 is 3/2. Multiplying these together, (2/3)

**(3/2) = 1.

Similarly, the reciprocal of 5/7 is 7/5. Again, (5/7)** (7/5) = 1.

Reciprocals of Integers

Integers can also have reciprocals. An integer can be thought of as a fraction with a denominator of 1.

For example, the integer 5 can be written as 5/1. Therefore, its reciprocal is 1/5.

The integer -3 can be written as -3/1, so its reciprocal is -1/3.

Special Cases and Considerations

Certain numbers present special cases when considering reciprocals. It's crucial to understand these exceptions to avoid errors.

Zero

Zero is unique because it has no reciprocal. Division by zero is undefined in mathematics. There is no number that you can multiply by zero to get 1.

Positive and Negative Numbers

Positive numbers have positive reciprocals. The reciprocal of 4 is 1/4, both of which are positive.

Negative numbers have negative reciprocals. The reciprocal of -2 is -1/2, both of which are negative.

One

The number 1 is its own reciprocal. Since 1 * 1 = 1, the reciprocal of 1 is 1.

The reciprocal, as a foundational concept, provides the stepping stone to grasping the idea of negative reciprocals. We've seen how inverting a number gives us its reciprocal, but what happens when we introduce negativity into the equation?

Demystifying Negative Reciprocals: Flipping and Negating

A negative reciprocal combines two simple mathematical operations to create a powerful tool. It is crucial for understanding concepts in geometry, physics, and engineering. Understanding negative reciprocals can unlock a deeper understanding of various mathematical and scientific applications.

Defining the Negative Reciprocal

The negative reciprocal of a number is simply the negative of its reciprocal. In other words, you first find the reciprocal of a number and then change its sign. If the original number was positive, its negative reciprocal will be negative, and vice versa.

This might seem overly simplistic. However, this two-step process is at the heart of its utility.

The Two-Step Process Explained

The process of finding a negative reciprocal always involves these two key steps:

1. Find the Reciprocal: Determine the reciprocal of the original number by inverting it (if it's a fraction) or expressing it as 1 divided by the number (if it's an integer).

2. Change the Sign: If the original number was positive, make the reciprocal negative. If the original number was negative, make the reciprocal positive.

Let's illustrate this with a few examples.

Examples with Fractions

Consider the fraction 3/4.

1. Find the Reciprocal: The reciprocal of 3/4 is 4/3.

2. Change the Sign: Since 3/4 is positive, its negative reciprocal is -4/3.

Therefore, the negative reciprocal of 3/4 is -4/3.

Another example: Let's find the negative reciprocal of -2/5.

1. Find the Reciprocal: The reciprocal of -2/5 is -5/2.

2. Change the Sign: Since -2/5 is negative, its negative reciprocal is 5/2.

So, the negative reciprocal of -2/5 is 5/2.

Examples with Integers

Let's consider the integer 2. Remember that any integer can be expressed as a fraction with a denominator of 1 (2/1).

1. Find the Reciprocal: The reciprocal of 2 (or 2/1) is 1/2.

2. Change the Sign: Since 2 is positive, its negative reciprocal is -1/2.

Thus, the negative reciprocal of 2 is -1/2.

Now, let's find the negative reciprocal of -5.

1. Find the Reciprocal: The reciprocal of -5 (or -5/1) is -1/5.

2. Change the Sign: Since -5 is negative, its negative reciprocal is 1/5.

Hence, the negative reciprocal of -5 is 1/5.

By consistently applying these two steps, you can confidently find the negative reciprocal of any number. This foundational understanding will be crucial when we explore its applications, especially in geometry.

The earlier discussions laid the groundwork for understanding what negative reciprocals are and how they're constructed. Now, let’s solidify that knowledge with a clear, step-by-step method for finding them. This structured approach will minimize errors and build confidence in tackling more complex mathematical problems.

Step-by-Step Guide: Finding Negative Reciprocals with Ease

This section provides a detailed guide on how to find negative reciprocals. This involves a three-step process. These steps, when followed carefully, will make this mathematical operation straightforward.

Step 1: Identify the Number

The first step is to clearly identify the number you're working with. This seems obvious, but it's crucial to note whether the number is positive or negative. This initial assessment dictates how you'll adjust the sign in the final step.

For instance, if you're given the number 5, you know it's positive. Conversely, if you see -2/3, you immediately recognize it as negative. Making this distinction upfront prevents errors later on.

Step 2: Find the Reciprocal of the Number

Once you've identified the number, the next step is to determine its reciprocal.

Remember, the reciprocal of a number is simply 1 divided by that number.

• For integers: If your number is an integer (like 5), its reciprocal is 1 divided by that integer (1/5).
• For fractions: If your number is a fraction (like 2/3), its reciprocal is found by inverting the fraction (3/2). The numerator becomes the denominator, and vice versa.

It's worth repeating: the reciprocal of a fraction is obtained by swapping its numerator and denominator. This simple maneuver is key to success.

Step 3: Change the Sign

This is the final, and arguably most critical, step.

Here, you change the sign of the reciprocal you just found.

If the original number was positive, the negative reciprocal will be negative. If the original number was negative, the negative reciprocal will be positive.

This sign change is what distinguishes a regular reciprocal from a negative reciprocal. Don't skip this step!

Examples to Illustrate the Process

Let's solidify these steps with some practical examples.

Example 1: Finding the Negative Reciprocal of 4

1. Identify the number: 4 (positive).
2. Find the reciprocal: 1/4.
3. Change the sign: -1/4 (the negative reciprocal).

Therefore, the negative reciprocal of 4 is -1/4.

Example 2: Finding the Negative Reciprocal of -2/5

1. Identify the number: -2/5 (negative).
2. Find the reciprocal: -5/2.
3. Change the sign: 5/2 (the negative reciprocal).

Therefore, the negative reciprocal of -2/5 is 5/2.

Example 3: Negative Reciprocal of 1

1. Identify: The number 1 (positive).
2. Reciprocal: The reciprocal is 1/1 = 1.
3. Change the sign: The negative reciprocal of 1 is -1.

Understanding these steps is crucial for more advanced applications involving negative reciprocals. Consistently applying this three-step process will solidify your understanding.

The earlier discussions laid the groundwork for understanding what negative reciprocals are and how they're constructed. Now, let’s solidify that knowledge with a clear, step-by-step method for finding them. This structured approach will minimize errors and build confidence in tackling more complex mathematical problems.

The Connection: Negative Reciprocals and Slope in Geometry

Negative reciprocals aren't just abstract mathematical concepts. They have a profound and practical application in geometry, specifically in understanding the relationship between lines and their slopes. This connection allows us to determine when two lines are perpendicular.

Slope: A Quick Review

Before diving into the connection, let's quickly recap what slope is. The slope of a line describes its steepness and direction. It's often referred to as "rise over run." Mathematically, it's the change in the y-coordinate divided by the change in the x-coordinate between any two points on the line.

A positive slope indicates that the line is rising as you move from left to right. A negative slope means it's falling. A slope of zero represents a horizontal line, and an undefined slope indicates a vertical line.

The Relationship Between Negative Reciprocals and Slope

The crucial relationship lies in how negative reciprocals describe the slopes of perpendicular lines.

Two lines are perpendicular if they intersect at a right angle (90 degrees). If you know the slope of one line, you can find the slope of any line perpendicular to it by calculating its negative reciprocal.

In essence, if one line has a slope of 'm', a line perpendicular to it will have a slope of '-1/m'. This negative reciprocal relationship is fundamental in coordinate geometry.

Perpendicular Lines: Identifying Them Using Negative Reciprocals

To determine if two lines are perpendicular, simply find their slopes. If the slopes are negative reciprocals of each other, then the lines are perpendicular.

Let's look at some examples:

• Example 1: Line 1 has a slope of 2. Line 2 has a slope of -1/2. Since -1/2 is the negative reciprocal of 2, the lines are perpendicular.

• Example 2: Line 1 has a slope of -3/4. Line 2 has a slope of 4/3. Because 4/3 is the negative reciprocal of -3/4, these lines are also perpendicular.

• Example 3: Line 1 has a slope of 1. Line 2 has a slope of -1. Since -1 is the negative reciprocal of 1, the lines are perpendicular.

Visualizing Perpendicularity

Imagine a coordinate plane. Draw a line with a slope of 2 (it rises steeply). Now, draw a line with a slope of -1/2 intersecting the first line. You'll see that they form a perfect right angle.

This visual representation helps solidify the concept: negative reciprocal slopes create perpendicular lines.

Special Cases: Horizontal and Vertical Lines

Horizontal and vertical lines are special cases that further illustrate this relationship. A horizontal line has a slope of 0. A vertical line is perpendicular to it and has an undefined slope.

Think of an undefined slope as being the reciprocal of zero (1/0), but also with a sign change that is irrelevant due to the nature of infinity. This underscores the negative reciprocal relationship, even in these extreme cases.

The relationship between a number and its negative reciprocal might seem straightforward, but it’s surprisingly easy to stumble. Let's explore some common errors to help you navigate these mathematical waters more confidently.

Avoiding the Pitfalls: Common Mistakes When Working with Negative Reciprocals

The Sign Slip-Up: Forgetting to Change the Sign

One of the most frequent errors is overlooking the "negative" part of "negative reciprocal." It's easy to correctly find the reciprocal of a number but then forget to flip its sign.

Remember, the negative reciprocal requires both finding the reciprocal and changing the sign.

For example, the reciprocal of 2 is 1/2. However, the negative reciprocal of 2 is -1/2. Don’t let that negative sign be an afterthought!

To avoid this, make it a habit to explicitly write down the negative sign as soon as you find the reciprocal. This simple step can significantly reduce errors.

Reciprocal Roadblocks: Errors with Fractions

Fractions introduce a slightly higher level of complexity.

The reciprocal of a fraction involves swapping the numerator and denominator. The mistake often occurs when people try to apply other operations or don't perform the swap correctly.

For instance, the reciprocal of 3/4 is 4/3. The negative reciprocal is therefore -4/3.

Be methodical. Double-check that you've flipped the fraction correctly before applying the negative sign.

Another common error arises when dealing with mixed numbers. Always convert a mixed number to an improper fraction before finding the reciprocal. For example, to find the negative reciprocal of 2 1/3, first convert it to 7/3, then find the negative reciprocal: -3/7.

The Zero Zone: A Special Case

Zero is a unique number that demands special attention. It doesn't have a reciprocal.

Why? Because the reciprocal of 0 would be 1/0, which is undefined.

Therefore, the concept of a negative reciprocal does not apply to zero. It's an important exception to remember.

Trying to apply the rules of negative reciprocals to zero will lead to mathematical impossibilities. Avoid this common mistake by recognizing that zero simply doesn't play in this particular sandbox.

Put Your Knowledge to the Test: Practice Problems

Now that you’ve journeyed through the fundamentals, intricacies, and potential pitfalls of negative reciprocals, it’s time to solidify your understanding. Working through practice problems is essential for converting theoretical knowledge into practical skill. Consider this section a mathematical workout, designed to strengthen your grasp of negative reciprocals through targeted exercises.

Sharpening Your Skills: A Variety of Practice Problems

To truly master negative reciprocals, you need to test your knowledge across a range of scenarios. We’ve compiled a set of problems that cover various types of numbers, from simple integers to more complex fractions. Working through these problems will help you identify any areas where you might need further review and build confidence in your abilities.

Integers:

1. Find the negative reciprocal of 5.
2. What is the negative reciprocal of -8?
3. Determine the negative reciprocal of 1.
4. Calculate the negative reciprocal of -10.
5. What is the negative reciprocal of 25?

Fractions:

1. Find the negative reciprocal of 2/3.
2. What is the negative reciprocal of -5/7?
3. Determine the negative reciprocal of 1/4.
4. Calculate the negative reciprocal of -9/2.
5. What is the negative reciprocal of 11/5?

Mixed Numbers:

1. Find the negative reciprocal of 1 1/2.
2. What is the negative reciprocal of -2 2/3?
3. Determine the negative reciprocal of 3 1/4.
4. Calculate the negative reciprocal of -1 3/5.
5. What is the negative reciprocal of 4 1/2? Remember to convert mixed numbers to improper fractions before finding the reciprocal.

Checking Your Work: Solutions for Self-Assessment

To ensure you’re on the right track, we’ve provided detailed solutions for each practice problem. Don’t just skip straight to the answers! Make a genuine effort to solve each problem on your own first. Then, carefully compare your solutions to ours, paying close attention to any discrepancies. Understanding why you might have made a mistake is just as important as getting the right answer.

Solutions: Integers

1. -1/5
2. 1/8
3. -1
4. 1/10
5. -1/25

Solutions: Fractions

1. -3/2
2. 7/5
3. -4
4. 2/9
5. -5/11

Solutions: Mixed Numbers

1. -2/3
2. 3/8
3. -4/13
4. 5/8
5. -2/9

Tips for Success

• Show your work: Writing out each step of the process can help you avoid careless errors and identify any points where you might be struggling.

• Double-check your signs: Remember that the negative reciprocal requires both finding the reciprocal and changing the sign.

• Practice makes perfect: The more you practice, the more comfortable you’ll become with finding negative reciprocals.

• Don't be afraid to seek help: If you're still struggling after working through the practice problems, don't hesitate to ask a teacher, tutor, or classmate for assistance.

By actively engaging with these practice problems and carefully reviewing the solutions, you'll not only solidify your understanding of negative reciprocals, but also develop valuable problem-solving skills that will serve you well in your mathematical journey. Good luck!

Video: Negative Reciprocal? Easy Guide You'll Wish You Knew!

Play Video