2-Sided Shape? The Shocking Truth You Need to Know!

Geometry, the branch of mathematics dealing with shapes, provides a framework for understanding spatial relationships. Euclid, a Greek mathematician often referred to as the 'father of geometry,' established foundational principles that still influence geometric study. However, when pondering what is a shape with 2 sides called, you might encounter some intriguing challenges, as conventional geometric definitions often preclude such a shape. Understanding these nuances is crucial for navigating the complexities of higher-level mathematics.

Image taken from the YouTube channel Jack Hartmann Kids Music Channel , from the video titled Shapes, Sides and Vertices | Version 1 | Jack Hartmann .
Geometry, at its core, is the study of shapes, sizes, relative positions of figures, and the properties of space. From the simple square to the complex dodecahedron, shapes form the bedrock of our understanding of the visual world.
They are more than just aesthetically pleasing forms; shapes are the language through which we describe and analyze the structure of everything around us.
But what happens when we push the boundaries of conventional geometry? What if we dare to question the fundamental building blocks upon which this entire system is built?
Posing the Question: A Two-Sided Enigma
Imagine, if you will, a shape with only two sides. What would it look like?
This isn't a riddle or a trick question. It's an invitation to explore the very essence of what defines a shape and its boundaries.
The query may seem simple, almost childish, yet it belies a depth of complexity that can challenge our most basic assumptions about geometry. This seemingly simple question forces us to confront our preconceived notions. It dares us to think outside the box, or perhaps, outside the polygon.
Our Objective: A Journey into Geometric Principles
This article embarks on a journey to unravel the surprisingly intricate answer to this question. We will delve into the definitions of shapes and sides, explore the possibilities (and impossibilities) of creating such a figure, and ultimately, understand why the answer is more nuanced than it initially appears.
It's a journey into the heart of geometric principles, where we'll discover that even the simplest questions can lead to profound insights. Together, we will explore the boundaries of what is geometrically possible.
Are you ready to begin?
Defining Our Terms: Sides and Shapes in Geometry
Before we can definitively answer whether a two-sided shape can exist, we must first establish a clear understanding of the fundamental terms at play: side and shape.

These words, seemingly simple and commonplace, hold specific and crucial meanings within the context of geometry and mathematics. A precise understanding of these terms will form the bedrock of our investigation.
What is a "Side" in Geometry?
In geometry, a side typically refers to a straight line segment that forms part of the boundary of a two-dimensional shape, also known as a polygon.
Consider a square: it has four sides, each a straight line segment connecting two vertices (corners). Similarly, a triangle has three sides.
These sides, when connected in a closed loop, define the extent and form of the shape itself.
However, the concept of a "side" isn't limited to straight lines. It can also refer to a curved line segment that contributes to forming a closed figure. Think of a circle, which we can consider being bounded by a curved line.
Classifying Shapes by Their Sides
Traditional Euclidean geometry classifies shapes primarily based on the number of sides they possess.
This is a fundamental way we categorize and understand different geometric figures.
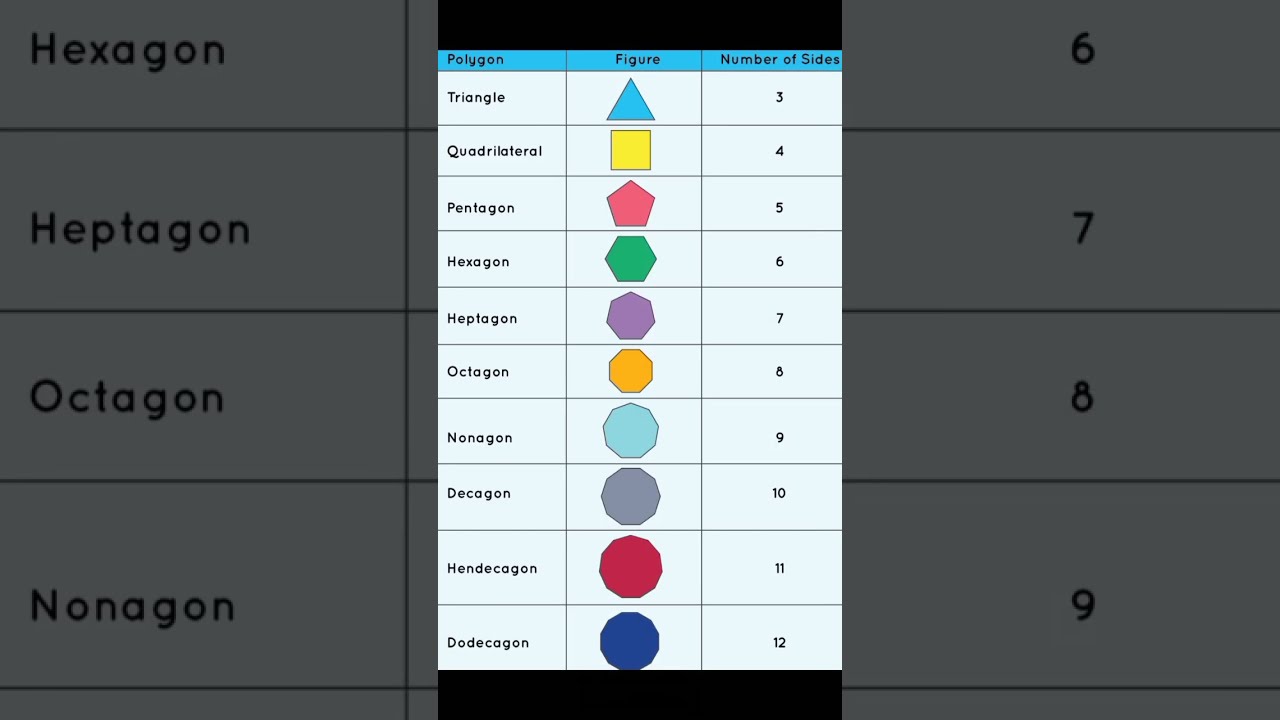
For example, polygons are named according to their sides:
- Triangles (3 sides)
- Quadrilaterals (4 sides)
- Pentagons (5 sides)
- Hexagons (6 sides) …and so on.
This classification system provides a structured framework for analyzing and comparing different shapes based on their fundamental structural components.
Shapes in Mathematics
Mathematics, in its broader sense, defines shapes through a more abstract and general lens.
It uses concepts from set theory, topology, and other branches to define shapes based on their properties, such as connectedness, boundaries, and dimensionality.
In mathematics, a shape can be any object that possesses a well-defined boundary and a set of spatial relationships between its points.
This definition allows for a much wider range of shapes to be considered, including those that may not conform to the traditional Euclidean notion of polygons with straight sides. It's a far more inclusive and powerful definition.
Exploring the Possibilities: Lines, Curves, and Closure
Having established the groundwork by defining our key terms, we can now embark on a crucial phase of our exploration: investigating whether two lines or curves can indeed create a closed shape. This requires us to challenge our initial assumptions and delve into the very nature of closure in geometric figures.
Straight Lines: An Impossibility of Closure
Can two straight lines form a closed shape? The answer, within the confines of Euclidean geometry, is a resounding no.
For a shape to be considered closed, it must fully enclose an area, creating a distinct boundary between the interior and exterior. Two straight lines, no matter how they are positioned, can never achieve this.
They might intersect, forming an angle, but they will always extend infinitely in at least one direction, failing to create a bounded region.
Consider two intersecting lines: they create four angles, but none of these angles are shapes in the geometric sense.
Even if the lines are parallel, they will remain open, never converging to form an enclosure.
Curves: A Glimmer of Potential
What if we move beyond straight lines and consider curves? Could two curves possibly define a shape? Here, the possibility, while still limited, becomes slightly more intriguing.
The key lies in the concept of arcs. An arc is a segment of a curve that connects two points. If two arcs are carefully constructed and joined together, they can indeed form a closed shape.
Imagine two semi-circular arcs, each curving in opposite directions. When joined at their endpoints, they create a lens-like shape, a "vesica piscis," or a football shape.
This shape, although formed by curves and not straight lines, fulfills the criteria of enclosure.
The Subtle Power of Definitions
Our understanding of this matter is profoundly influenced by how we define "shape" and "side".
Formal definitions, often used in mathematics, tend to be strict, emphasizing precise boundaries and adherence to established rules. These definitions often exclude figures formed by only two curves from being considered shapes in the purest sense.
However, informal definitions, those used in everyday language, might be more flexible. We might intuitively recognize the lens-like figure as a "shape," even if it doesn't perfectly align with the formal definition of a polygon.
This highlights the crucial role definitions play in shaping our understanding. Our perception of whether a two-sided shape exists hinges on the lens through which we view the geometric world.
Having explored the potential of lines and curves, and navigated the intricacies of closure, we now arrive at the crux of our investigation. It’s time to deliver the verdict, to address the existence of a two-sided shape, and to understand why, under conventional geometric rules, it remains an impossibility.
The Verdict: Why a Two-Sided Shape Doesn't Exist (Usually)
In the realm of traditional Euclidean geometry, the answer is definitive: a shape with two sides, as we commonly understand the term, simply cannot exist. This isn't merely a matter of semantics; it's rooted in the fundamental principles that govern how we define and construct shapes.
The Enclosure Requirement
The core reason a two-sided shape is a geometric anomaly lies in the very definition of a shape itself.
For a figure to qualify as a bona fide shape, it must fully enclose an area. It needs to create a clear and unambiguous boundary between the region inside the shape and the region outside.
Think of a circle, a square, or even a more complex polygon. Each of these has a defined perimeter that completely seals off its interior. This enclosure is non-negotiable.
Two lines or curves, no matter how ingeniously arranged, typically fail to meet this essential criterion. They might intersect, creating angles or arcs, but they cannot, in their simplest form, define a completely bounded region. There's always an opening, an escape route, preventing the formation of a true, closed shape.
Euclidean Geometry vs. Topology: A Shift in Perspective
It's important to acknowledge that our conclusion is largely based on the rules of Euclidean geometry – the system we learn in schools, dealing with flat surfaces and familiar shapes.
However, mathematics is far from monolithic. There exist other branches, like topology, that challenge these rigid constraints.
Topology, sometimes called "rubber sheet geometry," is concerned with properties that are preserved through continuous deformations, such as stretching, twisting, crumpling, and bending.
In topology, the notion of shape becomes far more flexible. A coffee cup and a donut, for example, are considered topologically equivalent because one can be transformed into the other without cutting or gluing.
While topology offers a fascinating alternative perspective, it doesn't fundamentally alter the impossibility of a two-sided shape within the strict confines of Euclidean geometry.
The Role of Angles
Angles are crucial components in the formation of shapes within Euclidean geometry. They represent the measure of the space between two intersecting lines or surfaces at or close to the point where they meet.
In traditional polygons, angles are formed where sides connect to create vertices, contributing to the enclosure and definition of the shape.
If a two-sided shape were to exist, the question of how angles could form with only two sides arises. Without a third side, the conventional understanding of an angle as the space between two intersecting lines becomes problematic.
Any shape existing with only two sides would require a reconceptualization of how angles define enclosure and shape. It suggests that even if lines were joined perfectly, they do not create an enclosed, bounded shape.
Having established the conventional geometric perspective, which firmly denies the existence of a two-sided shape, it's time to venture beyond these established boundaries. Are there situations or contexts where our understanding of "shape" and "side" can be stretched, redefined, or even circumvented? Let’s look into the world of exceptions and advanced concepts.
Beyond the Basics: Exceptional Cases and Advanced Concepts
While Euclidean geometry provides a solid framework, the world of shapes isn't always so black and white. There are instances where our intuitive understanding of "shape" might lead us to question the strict rules. Let's explore some exceptional cases and advanced concepts that challenge conventional geometric thinking.
The Lunes of Hippocrates: A Glimpse of Curvilinear Boundaries
Consider the Lunes of Hippocrates, named after the ancient Greek mathematician. These are crescent-shaped areas bounded by two circular arcs.
While not a two-sided shape in the strictest sense, the lune offers a compelling example of how curvilinear boundaries can define a region in a way that feels intuitively like a shape.
Each boundary is an arc, curving to create the shape.
The lune doesn't fully enclose an area with just two sides meeting our initial criteria, but it demonstrates how curved lines can create a boundary and an area.
The Ambiguity of "Side": Reconsidering the Definition
Perhaps the issue lies not in the possibility of a two-sided shape, but in our definition of "side." Is a side necessarily a straight line segment? What about a curve that continuously changes direction?
This opens the door to a more nuanced interpretation, blurring the lines (pun intended) between sides and boundaries.
Approaching Infinity: A Thought Experiment
Imagine a shape where the two "sides" are infinitely long lines that asymptotically approach each other, never actually meeting but defining a region between them.
Would this qualify as a two-sided shape? It's a question that pushes the boundaries of our geometric intuition. While it may not meet the strict definition of enclosure, the concept prompts us to consider the limitations of our finite understanding.
The Moon: A Familiar Shape with a Complicated Boundary
Think of a crescent moon. It certainly appears to have two sides, defined by the curves of its illuminated and shadowed edges.
However, neither of these edges exists independently. The moon's crescent is a result of perspective and illumination, not an inherent two-sided structure.
The moon, however, highlights that our perception of shape is influenced by factors beyond pure geometry, like light, shadow, and the position of the observer. It demonstrates the gap between how we see shapes and how geometry defines them.
Video: 2-Sided Shape? The Shocking Truth You Need to Know!
FAQs About 2-Sided Shapes
Still scratching your head about shapes with two sides? This FAQ section breaks down the concept and clarifies any confusion surrounding this unusual geometrical idea. Let's dive in!
Can a shape actually have only two sides?
The short answer is no. In Euclidean geometry, shapes are typically defined as being enclosed. A shape must have at least three sides to form a closed figure. Therefore, a true shape cannot exist with only two sides.
So, what is a shape with 2 sides called if it's not a real shape?
There isn't a formally recognized name in standard geometry for a shape with only two sides. Because it cannot form a closed figure, it doesn't qualify as a traditional shape. The concept is more of a theoretical consideration.
Why do some discussions talk about 2-sided shapes?
These discussions usually explore the boundaries of geometric definitions or delve into more abstract mathematical concepts. Thinking about "impossible" shapes can help us better understand the rules that define legitimate geometric figures.
Could advanced math or other dimensions allow for a 2-sided shape?
While in standard Euclidean geometry, it's impossible, some advanced mathematical theories or hypothetical scenarios involving extra dimensions might allow for definitions that could be interpreted as resembling something like a two-sided shape. This is far outside the scope of typical geometry however.
So, there you have it! Hopefully, this cleared up any confusion about what is a shape with 2 sides called. Happy shape-exploring!